1. F分布

1.1. F 分布的概念

  • F分布是以现代统计学的奠基人R.Fisher命名的。
  • 对于以下两种情况，我们用F概率分布作为检验统计量：
    • 用于检验样本是否来自具有相同方差的总体
    • 比较⼏个总体的均值anova
  • 前提条件：总体必须满足正态分布 。

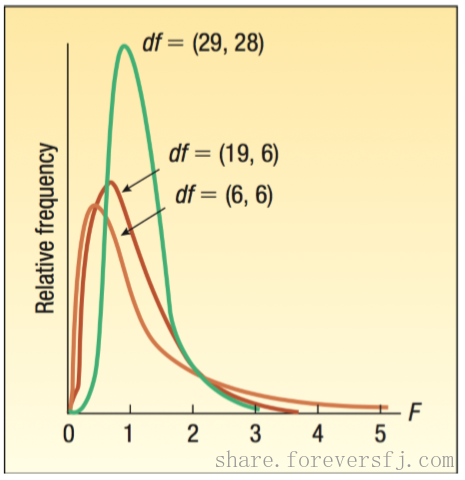
1.2. F分布的特征

  • F分布是一族分布，F分布族的一个特定的分布是由两个参数确定：

    分⼦的自由度 和 分母的自由度 。

  • F分布是连续的，数值∈ [0,∞）

  • F分布不能是负值，最小值可以假定是0

  • F分布是右偏分布，长尾在右侧，随着分子和分母自由度的增加，F分布近似于一个正态分布

  • F分布是渐近分布, 随着X的增加，F曲线趋向于X轴，但绝不与X轴相交

2. 比较两总体的⽅差

2.1. 统计量

  • F分布用于检验：一个正态总体的方差与另一个正态总体的方差相等。

  • 假设条件：$H_0: \alpha_1^2=\alpha_2^2$，$H_1: \alpha_1^2≠\alpha_2^2$

  • 统计量：$F(n_1,n_2) = \frac{S_1^2}{S_2^2}$

  • 为了减少临界值表的大小，通常将较大的样本方差放在分子位置。

  • 所以，对于一个双侧检验，通常只需要右侧的临界值。

3. ANOVA检验

3.1. 检验条件

  • anova用于检验3个或3个以上的总体的均值是否相等
  • 假设条件：
    • 总体服从正态分布；
    • 总体标准差相等；
    • 总体是独立的。
  • anova允许我们同时比较多个样本的均值和避免犯第⼀类错误可能性的叠加。

公式概念

  • $处理平方和=\sum_{处理个数}{(区组个数)*(处理的每一个值-处理均值)^2}$
  • $F统计量的临界值：F(显著性水平)=\frac {分子自由度} {分母自由度}$
  • $分子自由度：处理个数k减1，k-1$
  • $分母自由度：观测值的总个数n减处理个数k，n-k$

双因素方差分析