抽样与中心极限定理
条评论1. 抽样方法
1.1. 抽样的理由
- 联系总体将会花费大量的时间
- 对总体的所有项目进行研究的成本过高
- 对总体的所有项目进行检验实际不可能
- 一些检验实验具有破坏性
- 样本结果是充分的
1.2. 简单随机抽样
简单随机抽样:使得总体中的每个单元或者个体都有相同的机会被选中的方法抽取的一个样本。

1.3. 系统随机抽样
系统随机抽样:随机选取一个起始点,然后每第k 个总体单位被抽去出来进入样本。
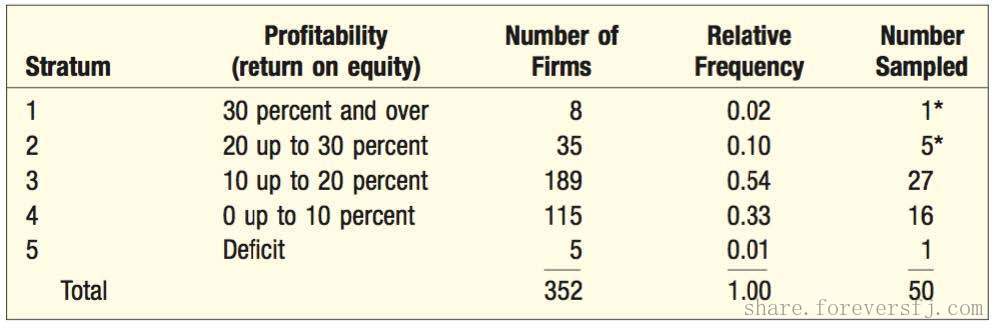
1.4. 分层随机抽样
分层随机抽样:总体被分成若干个组,每一组被称作一层,并且从每一层里随机的抽取一个样本。
1.5. 整群抽样
整群抽样:利用自然形成的地理的或其他的界限将总体分成群。然后,随机地抽取若干群并且从每个群里随机的抽取一个样本。

2. 抽样误差
抽样误差:一个样本统计量与其所对应的总体参数之间的差异。
3. 样本均值的抽样分布
一个给定样本容量的所有可能的样本均值的概率分布。
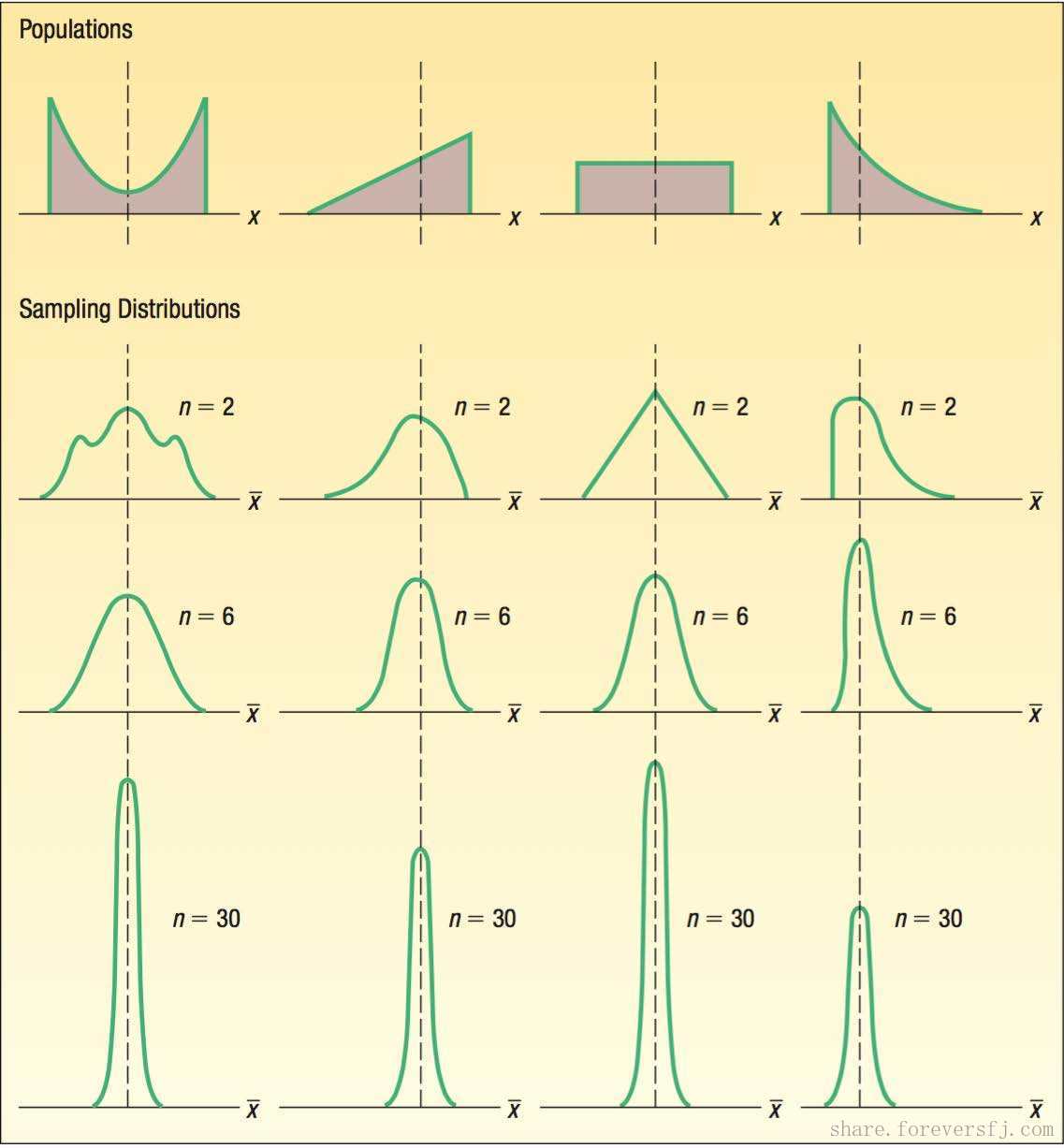
3.1. 中心极限定理
3.2. 定理
中心极限定理(central limit theorem):设从均值为 $\mu$,方差为 $\sigma ^ 2$ 的任意一个总体中抽取样本容量为 $n$ 的随机样本,则当 $n$ 充分大时,样本均值 $\bar X$ 的抽样分布近似满足均值为 $\mu$,方差为 $\sigma ^ 2/n$ 的正态分布。
3.3. 正态分布(高斯分布)
正态分布的密度函数::$f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$,$\sigma>0$
正态分布的期望和方差::$E(X)=\mu$,$Var(X)=\sigma^2$
3.4. 中心极限定理的说明
- 当总体服从正态分布时,无论样本大小,中心极限定理均适用;
- 当 $n \geq 15$ 时,对于分布较为对称的总体,中心极限定理适用;
- 当 $n \geq 30$ 时,无论总体分布形态如何,中心极限定理均适用;
- 从一个给定的总体中,抽取容量相同的所有可能的样本,样本均值(抽样分布的平均值)恰好等于总体均值。即:$\mu = \mu \bar X$;
- 样本均值抽样分布的离散程度将会比总体的离散程度小。并且,随着样本容量的增大,样本均值分布的标准差将减少。
4. 样本均值抽样分布的应用
- 抽样的均值服从正态分布

本文标题:抽样与中心极限定理
文章作者:foreverSFJ
发布时间:2019-06-18 21:39:11
最后更新:2019-06-18 21:39:11
原始链接:Course/ManagementStatistics/抽样与中心极限定理.html
版权声明:本博客所有文章除特别声明外,均采用 CC BY-NC-ND 4.0 许可协议。转载请注明出处!
分享
